Calibration and uncertainty analysis

Koen Hufkens

Data preparation and filtering

Loading the formatted data (see data-raw scripts), and filtering only the harvard data as a demonstration.

# load libraries and functions
library(dplyr)
library(tidyr)
library(ggplot2)
library(patchwork)
library(BayesianTools)
source(here::here("R/likelihood.R"))
source(here::here("R/chlorophyll_cycling.R"))
source(here::here("R/df_to_list.R"))
source(here::here("R/normalize_ts.R"))
set.seed(0)

# load raw (bulk data)
# and filter for a single site
# and a DOY range
# further subsets can be generated
# using custom filters
# this is beyond the scope of this example
raw_data <- readRDS(here::here("data/phenocam_data.rds")) |>
  filter(
    site == "harvard"
    )|>
  group_by(year) |>
  mutate(
    gcc = normalize_ts(gcc, c(0.1,1)),
  ) |>
  filter(
    doy > 213
  )

# reformat to the required list based
# model input format
df <- raw_data |>
  df_to_list()

Setup {BayesianTools} routines / parameters for optimization. Note that this might take a while to run.

# Bayesian optimization routine
control = list(
  sampler = 'DEzs',
  settings = list(
    burnin = 1000,
    iterations = 100000
  )
)

# set parameter ranges
# b1 - b3
lower <- c(-1, 0, 0)
upper <- c(1, 1, 1)

# setup of the BT setup
setup <- BayesianTools::createBayesianSetup(
  likelihood = function(random_par){
    do.call("likelihood",
            list(par = random_par,
                 data = df,
                 model = "chlorophyll_cycling"
            ))},
  # include an additional parameter
  # range for data uncertainty
  lower = c(lower, 0),
  upper = c(upper, 2)
)

# calculate the optimization
# run and return results
out <- BayesianTools::runMCMC(
  bayesianSetup = setup,
  sampler = control$sampler,
  settings = control$settings
  )

Plot parameter traces

plot(out)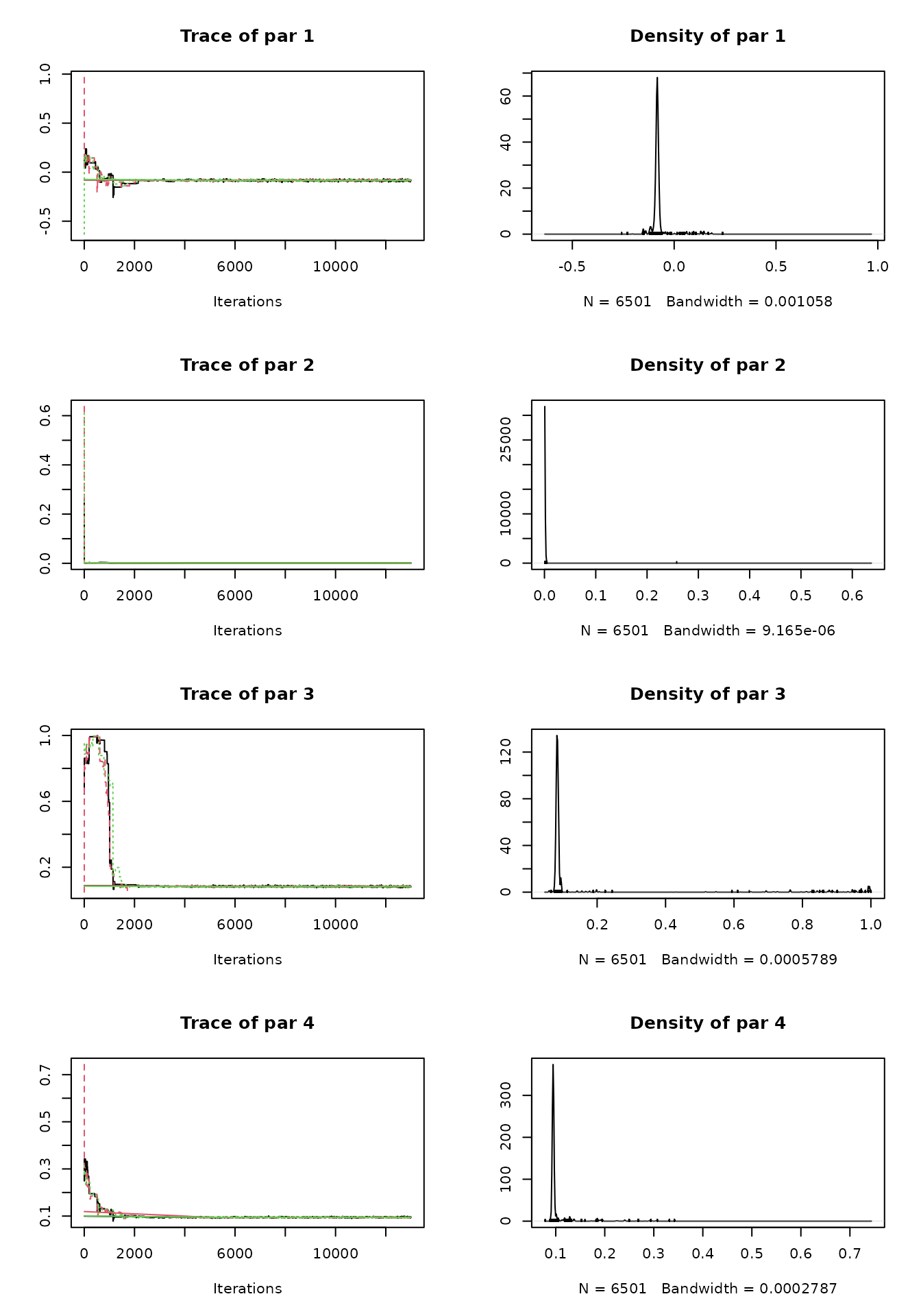

Gelman-Brooks-Rubin diagnostics

BayesianTools::gelmanDiagnostics(out)

## Potential scale reduction factors:
## 
##       Point est. Upper C.I.
## par 1       1.01       1.02
## par 2       1.01       1.02
## par 3       1.00       1.00
## par 4       1.01       1.02
## 
## Multivariate psrf
## 
## 1.01

Explore model results and uncertainty

# Sample parameter values from the posterior distribution
samples_par <- BayesianTools::getSample(
  out, 
  thin = 1000
  ) |>  
  as.data.frame() |>
  dplyr::mutate(
    mcmc_id = 1:n()
    ) |>
  tidyr::nest(
    .by = mcmc_id,
    .key = "pars"
    )

A wrapper for the model run (formatting the data).

model <- function(sample_par, data){
  gcc <- chlorophyll_cycling(
    par = sample_par,
    data = data
    ) |>
    as.data.frame()

  # doy label
  gcc$doy <- 1:nrow(gcc) + 212
  
  # convert to long format
  # inefficient but allows for nicer plotting
  gcc <- gcc |>
    tidyr::pivot_longer(
      starts_with("harvard"),
      values_to = "gcc"
      ) |>
    mutate(
      gcc_obs = gcc + rnorm(
        n = n(),
        mean = 0,
        sd = sample_par$`par 4`
      ),
      year = as.numeric(gsub("harvard_", "", name))
    )
}

Run the model across sampled parameters.

# Run the model for each set of parameters
model_runs <- samples_par |>
  dplyr::mutate(
    sim = purrr::map(pars, ~model(.x, data = df))
    )

Summarize the data by year and day-of-year.

model_runs <- model_runs |>
  tidyr::unnest(sim) |>
  dplyr::group_by(year, doy) |>
  dplyr::summarise(
    gcc_q05 = quantile(gcc, 0.05, na.rm = TRUE),
    gcc = quantile(gcc, 0.5, na.rm = TRUE),
    gcc_q95 = quantile(gcc, 0.95, na.rm = TRUE),
    gcc_obs_q05 = quantile(gcc_obs, 0.05, na.rm = TRUE),
    gcc_obs_q95 = quantile(gcc_obs, 0.95, na.rm = TRUE),
    .groups = "drop"
  )

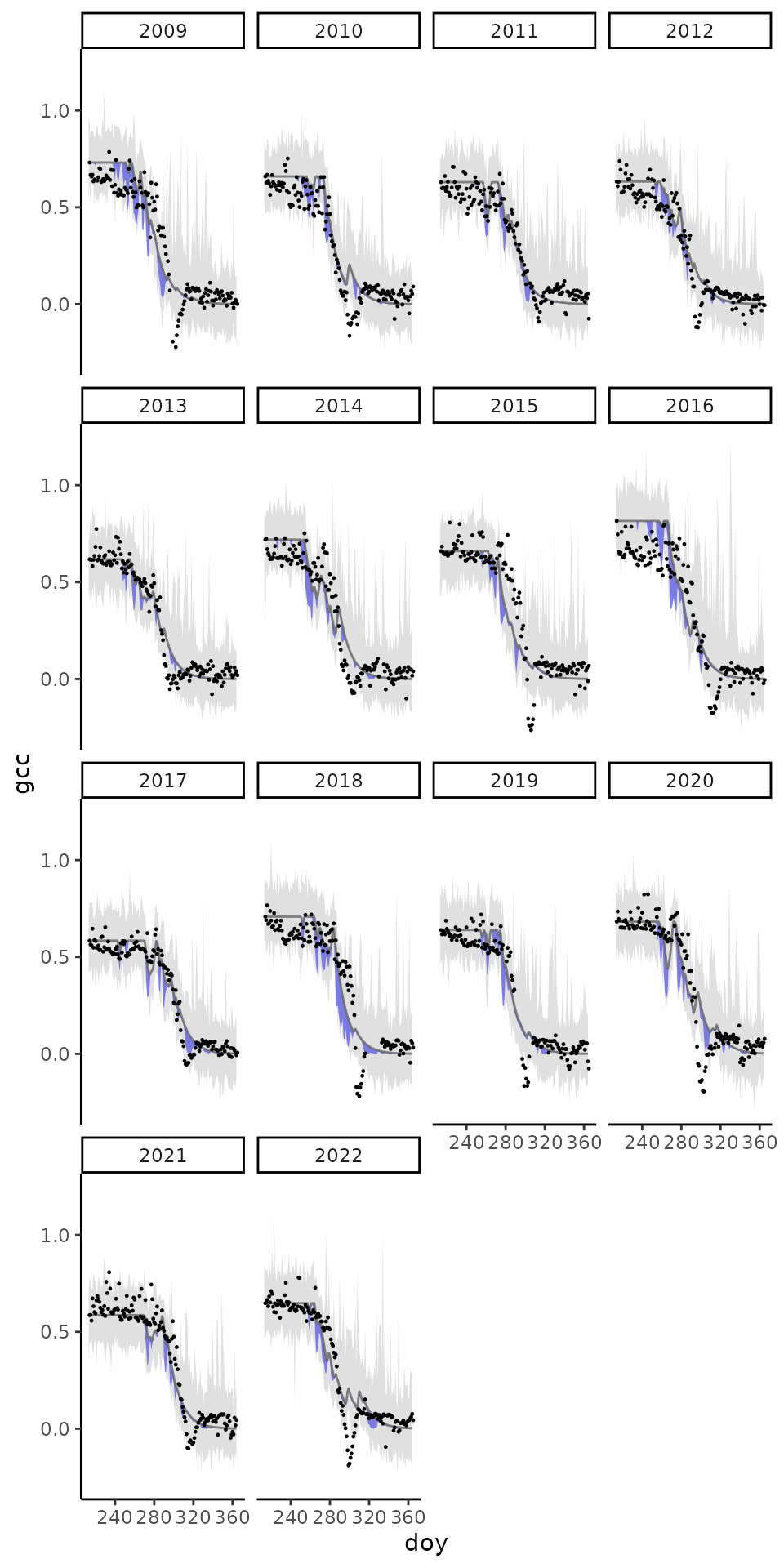
Plot the time series and uncertainties nicely. With grey, data uncertainty, and blue model uncertainty.

# Plot the credible intervals
plot_gcc_error <- ggplot(
  data = model_runs
  ) +
    geom_ribbon(
    aes(
      ymin = gcc_q05, 
      ymax = gcc_q95,
      x = doy
    ),
    fill = 'blue', alpha = 0.5) +
  geom_ribbon(
    aes(
      ymin = gcc_obs_q05, 
      ymax = gcc_obs_q95,
      x = doy
    ),
    fill = 'grey40', alpha = 0.2) +
  geom_line(
    aes(
      doy,
      gcc
    ),
    colour = "grey40",
    alpha = 0.8
  ) +
  geom_point(
    data = raw_data,
    aes(
      doy,
      gcc
    ),
    size = 0.2
  ) +
  theme_classic() +
  facet_wrap(~year)


print(plot_gcc_error)